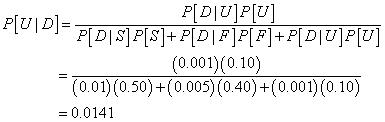An insurance company issues life insurance policies in three separate categories: standard, preferred, and ultra-preferred. Of the company’s policyholders, 50% are standard, 40% are preferred, and 10% are ultra-preferred. Each standard policyholder has probability 0.010 of dying in the next year, each preferred policyholder has probability 0.005 of dying in the next year, and each ultra-preferred policyholder has probability 0.001 of dying in the next year.
A policyholder dies in the next year.
What is the probability that the deceased policyholder was ultra-preferred?
- 0.0001
- 0.0010
- 0.0071
- 0.0141 Correct Answer
- 0.2817
Solution: D
Let
S = Event of a standard policy
F = Event of a preferred policy
U = Event of an ultra-preferred policy
D = Event that a policyholder dies
Then